
Pi Via PRNG
605 words. Time to Read: About 6 minutes.I just found something amazing out. It’s not that amazing. But it is neat. I’m going to build to it in an unnecessarily dramatic and roundabout way.
Coprimes
Let’s start with a concept called “Coprimacy”. Two numbers can be said to be coprime if they share no factors except one. For example, consider 75 and 28. The factors of 28 are 1, 2, 4, 7, 14, and 28. The factors of 75 are 1, 3, 5, 15, 25, and 75. Since the only one that is the same is 1, 28 and 75 are coprime. On the other hand, consider 24 and 64. The factors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24, while the factors of 64 are 1, 2, 4, 8, 16, 32, and 64. They actually share 1, 2, 4, and 8! These numbers are not coprime.
Coprimes, Everywhere
So let’s take this a bit further. I wonder what the odds are that two random numbers are coprime. Since I’ve got a buddy named Python, let’s take this a lot further!
# coprimes.py
from math import gcd
from random import randint
def is_coprime(first, second):
"""Return true if the first and second are coprime i.e. largest
common factor is 1"""
return gcd(first, second) == 1
def coprime_probability(limit, times):
"""Estimates the probability of two numbers being coprime via randoms"""
coprime_count = 0
for test in range(times):
a = randint(1, limit)
b = randint(1, limit)
if is_coprime(a, b):
coprime_count += 1
return coprime_count / times
if __name__ == "__main__":
print("Probability approximately:", coprime_probability(1000000, 1000000))When I run it, I get ~ 0.6075. So right now, I can hear a good portion of you actually giggling with excitement. “How could this possibly get any more interesting?” you ask in earnest. Here’s how.
The Reveal
Get ready because the next part is going to knock your socks off. Simply find the following: sqrt(6/coprime_probability). What do you get? 3.14! Don’t believe me? Let’s up the number of trials.
from matplotlib import pyplot as plt
import numpy as np
trials = np.array([100, 1000, 10000, 100000, 1000000, 10000000])
results = np.array([coprime_probability(1000000, trial) for trial in trials])
pi_values = np.array([math.sqrt(6/result) for result in results])Now let’s plot it.
plt.plot(trials, pi_values, "ro")
plt.xscale("log")
plt.show()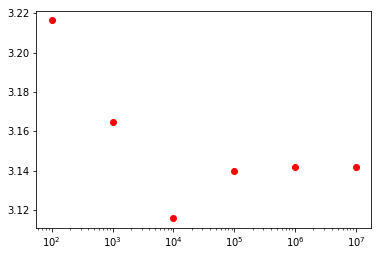
print(pi_values)[ 3.2163376 3.16491619 3.11588476 3.13967487 3.14168852 3.1420532 ]
So there you go! You just derived pi from a bunch of random numbers. You’re welcome!
Author: Ryan Palo | Tags: math python tricks | Buy me a coffee
Buy me a coffee
Like my stuff? Have questions or feedback for me? Want to mentor me or get my help with something? Get in touch! To stay updated, subscribe via RSS